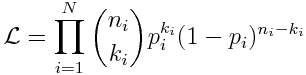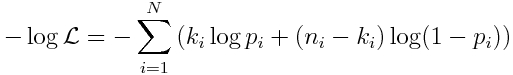[This is part of a series of modules on optimization methods]

The Binomial distribution is the probability distribution that describes the probability of getting k successes in n trials, if the probability of success at each trial is p.  This distribution is appropriate for prevalence data where you know you had k positive results out of n samples. Your model estimates the probability of success, p, which depends on the model parameters.

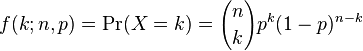
If we have a set of N data samples k_i and n_i (where i=1,…,N) and model estimates at those points p_i, the overall likelihood is

and the negative log-likelihood is (note that we can ignore the n_i choose k_i term because it only depends on the data, not the model):

An example of the an appropriate use of the Binomial likelihood:  I have a data time series of the number of tests for avian influenza on chicken flocks taken each month, and the number of those tests that were positive.  In this case, I could use an SIR model to estimate the model prediction for the prevalence, I (ie; the probability of a positive test, p), and this estimate of the prevalence depends on my model parameters, such as the transmission rate, and/or recovery rate.  The best-fit transmission rate and recovery rate minimize the Binomial negative log-likelihood.