[This is part of a series of modules on optimization methods]

Once you have a figure-of-merit statistic for how well your model fits your data (for instance, a Least Squares or a Poisson negative log-likelihood statistic), we want to find the model parameters that minimize that statistic.  Lets call this goodness of fit statistic S(theta), where theta is the vector of parameters upon which our model depends (and thus on which the goodness-of-fit parameter depends).

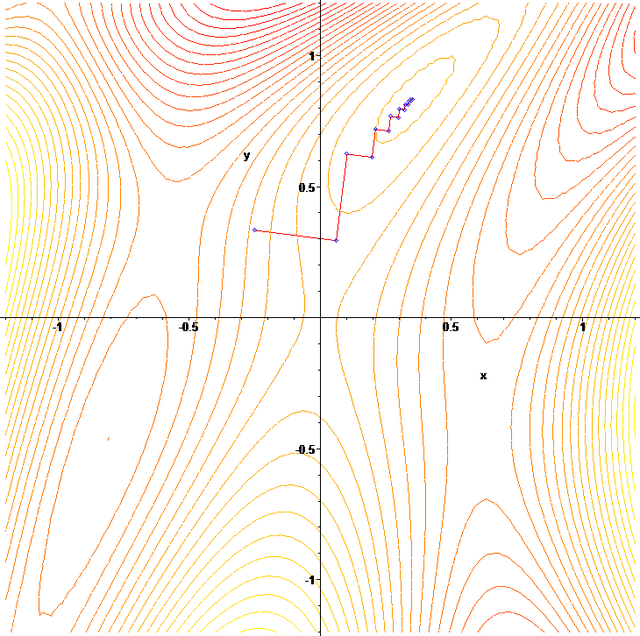
From calculus, we know that S will be locally maximized/minimized (as long as S is differentiable) when the gradient is equal to zero.  To find the minimum of a function using the gradient descent method, you first start with an initial guess of the location of the minimum, theta_0.  You calculate the gradient at that point.  You then choose new parameters in the direction of steepest descent (ie; the direction in which the negative of the gradient is largest).  The step size for each of the parameters depends on the value of the gradient at that point.  This is known as a gradient descent method, or method of steepest descent.  There are lots of extensions to the method.

Gradient descent methods tend to have limited applicability to problems in epidemiology/biology where we wish to fit the parameters of a non-linear system of ODE’s to data.  Here are some of the issues that arise

• You need to calculate the gradient of the goodness-of-fit statistic S at each step.  S depends on the model.  This necessitates calculating the gradient of the model at each step, which in turn involves the mother of all partial derivative calculations (particularly when multiple parameters are being optimized), not to mention numerically solving for the gradient at each step (because there is generally no closed form solution for the mathematical models we use).
• As you can see in the plot above, depending on your starting guess for the parameters, the gradient descent procedure can walk to a local, rather than global, minimum.  In my experience in trying to apply gradient descent methods in epidemiology/biology, the goodness-of-fit statistic often has local minima (I determine this by using parameter sweep methods, which we will discuss later).
• Sometimes the procedure never converges to an answer, but rather just keeps hopping back and forth to points in the vicinity of a minimum.
• There is no good graphical way to determine that the procedure has walked to a global, rather than local, minimum in S.
• The procedure cannot be readily parallelized to use distributed computing resources to speed up the computation time.
• No good way, post-hoc to all the computational complexity involved, to include constraints from Bayesian prior-belief on the model parameters in the analysis.  You have to include the constraints into the goodness-of-fit statistic right from the very beginning.