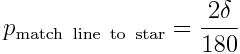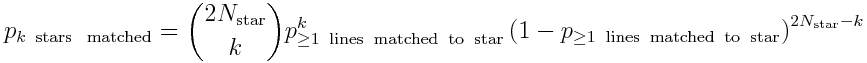[This post is part of a series of posts on archaeoastronomy using open source software]

In these modules, we’ve been considering the problem of archaeological sites that we posit may have been observatories of the rise/sets of celestial bodies. “Site lines” are lines drawn between salient features of a site that we posit might have been used to sight along to look at a particular point on the horizon.

The problem with a site that has many associated site lines is that there is a high probability some of those site lines will line up with the rise/set azimuth of a star just by mere random chance.  Alternatively, if we try matching site lines to the rise/set azimuths of many different stars (plus the Sun solstices and major and minor Moon standstills), we will get matches just by mere random chance.  It is a very common mistake to dramatically underestimate these spurious match probabilities, and take as a given that whatever matches we observe must be evidence that the site was used as an observatory.

Probability of getting spurious matches

Mathematically, we can calculate the probability of spurious matches.  Say we have a total number of site lines, N_lines (no cheating!  you have to consider all potential site lines, not just ones you cherry pick to match your hypothesis that the place was an observatory), and a total number of celestial bodies that we will consider the site might have been looking at, N_star. The total number of rise and set azimuths is thus 2*N_star.  Let’s assume that we consider a line a “match” to a rise or set azimuth if the angle between them is less than delta (so the site line is within -delta to +delta of the rise or set azimuth).  The probability of getting a spurious match of a particular site line to the star rise or set azimuth just by accident is thus

The probability that we get at least one of all the lines at a site spuriously matched to a star is 1 minus the probability that none of the site lines matched to the star:

(eqn 1)

Notice that as N_lines gets large, this probability can get close to one!

The probability that either the rise or set azimuth of k of the stars will be spuriously matched to at least one site line each is calculated from the Binomial probability distribution:

The probability of observing several spurious matches when you have a lot of stars and/or a lot of site lines can be rather large!

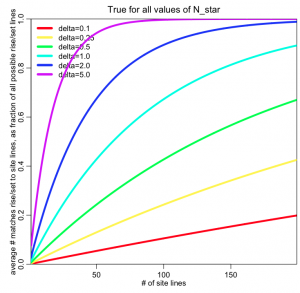
In this plot, I show the calculation, using the formulas above, for the average fraction of all rise/set lines that are spuriously matched to site lines (what is interesting is that it turns out that this fraction is independent of N_star!):

The plot above was made by the R script prob_spurious.R. You can see that there is a big increase in the probability of spurious matches when N_lines goes up, and/or when delta goes up (recall from above that 2*delta is the angular range we consider for a site line to “match” with a rise or set azimuth).  In archeoastronomy_libs.R there is a function expected_number_spurious(N_lines,N_star,delta) that calculates the expected number of spurious matches and the upper 95% confidence interval for that (it turns out that while the average fraction of spurious matches doesn’t depend on N_star, the upper 95% confidence interval does).

You may wonder why I included delta=5 degrees in the above plot, when it looks like such a large delta would make the probability of spurious matches far too high.  But I have actually seen some analyses that “match” site lines to rise/set azimuths with delta’s almost this high.  I’ll show an example…

Example: Big Horn Medicine Wheel

The Big Horn Medicine Wheel is a circular array of rocks on top of a remote mountain ridge in Wyoming, thought to be 300 to 800 years old:

The array of rocks is about 80′ in diameter, and has 28 radial spokes. In the 1970’s an astronomer, Dr. John Eddy, visited the site and examined the alignments.  He concluded that several alignments to stars were evident.

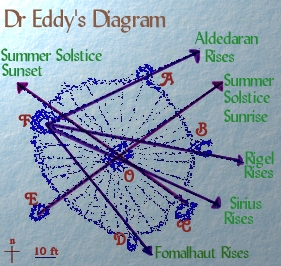
I count 21 different possible site lines between the cairns.  The faintest star for which there is a purported alignment is Fomalhaut, with a visual magnitude of around 1.2.  There are 13 stars with magnitude<=1.2 that visibly rise and set at the latitude of the medicine wheel.  Add in the possible interesting sun and moon rise/set azimuths, and we get N_star=18.

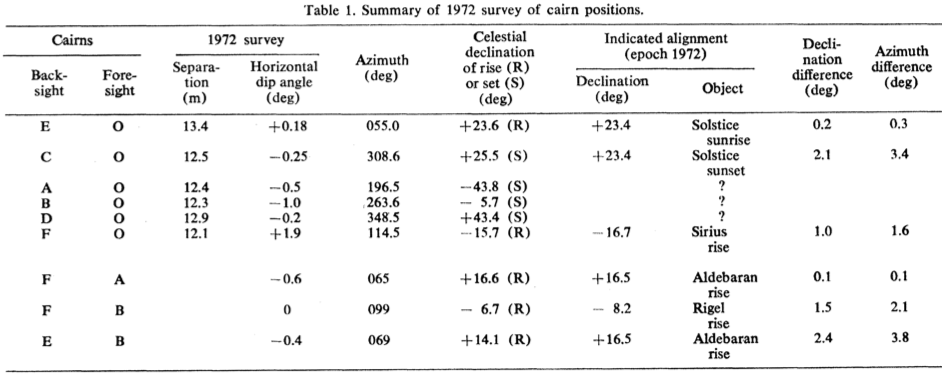
Dr.Eddy appears to have used a very large value of delta to consider a site line and a star rise/set azimuth to have “matched”.  Here is a table from his paper:

You can see that he was using a delta of up to 3.8;  from the plot I showed in the previous section, it looks like, conservatively, he would have expected around 30% of all the possible rise/set azimuths to spuriously match with site lines when delta is that high and with 21 possible site lines.  He got 7 out of 36 possible rise and set azimuths matching to site lines, which is statistically consistent with the 30% expected just by mere random chance.

Was the Big Horn Medicine Wheel used as an astronomical observatory?  Maybe.  But statistically speaking, we have no way to say that there is significant evidence that it was.

Possible Solutions to the Folly of too many Lines

In order to reduce the probability of spurious matches between site lines and rise/set azimuths of stars, one can either reduce delta, and/or reduce the number of possible site lines at a particular site.  One way to achieve both is to only consider site lines that are drawn between several key points at a site (rather than just two).  With multiple points, the uncertainty on which way the line is pointing goes down, and also there are (presumably) a lot fewer site lines that meet the criteria.

As I described in this post, to assess whether or not a site line fit to multiple points actually is a good fit, I use fits to points to randomly scrambled versions of the site to determine the probability distribution for a goodness-of-fit statistic;  I then make the selection in this statistic such that only a small fraction of the lines fit to the randomly scrambled points pass the selection.  In this way, if lines fit to the original site configuration pass this selection, I can be quite confident that the apparent alignment didn’t happen by mere random chance.

Uncertainty on the rise/set azimuths of the stars can also be reduced by knowing the exact date of the construction of a site, and through a careful survey of the horizon dip angles.  However, I would be surprised if the net uncertainty from these two sources can ever be reduced to below delta=0.1 degrees for any site.

And remember… no cheating!  You need to decide before you start an analysis of a site how many datum points at the site are needed per each site line.  As an aside though, I think it is a bad idea to consider site lines connecting just two points; you can always draw straight lines between any two points, so the probability you end up with a set of spurious site lines with no real relationship to star rise/set azimuths is high.

Another way you can reduce the probability of spurious matches is to require that you will only consider a star to be observed at a site if the site has alignments to both the rise and the set azimuth of the star. That means instead of Equation 1, we get that expression squared.  This has the potential to dramatically reduce the probability of spurious matches.   But, again… no cheating.! You have to decide before you start your analysis that you will require a star to be considered to be observed if only both its rise and set azimuths have alignments at the site.

One other interesting thing to look at is how many stars in your “potential stars” list have neither their rise nor set azimuths aligned to site lines.  If this number is unusually high compared to the number we’d expect from mere random chance, and if the only stars that do have alignments have alignments to both the rise and the set azimuths, it can indicate that the site was carefully set up to just look at those stars, and no others (ie; they were purposefully avoiding having their site line up in any way with stars they were not interested in!).