If you are looking at an archaeological site that you believe was a comprehensive ancient sky observatory, it may be possible to date the site from its alignments to celestial phenomenon.  Note that you need a site with several likely sun/moon/star alignments to do this. On this page I provide some handy R and python scripts to calculate the rise/set azimuth (assuming a flat horizon) of the Sun, Moon, and stars for a given location at a given date.

For a given latitude, the rise and set azimuths of the sun and moon change slowly over time due to effects of axial precession and nutation that change the inclination angle of the Earth’s rotational axis with respect to the ecliptic (known as the ‘obliquity’).  Laskar (1986) developed a formula that provides a good approximation for the obliquity going back many thousands of years:

In the R script sun_moon.R I use the Laskar formula to calculate the rise and set azimuths (the azimuth is the degrees from north on the horizon that the celestial body rises or sets at) of the sun summer and winter solstices, and the major and minor moon northern and southern standstills.  The calculation is done for years going from 5000 BC to present in steps of 1000 years, and is done for latitudes from 20 to 55 degrees north in steps of 5 degrees (20 degrees North is the approximate latitude of Mayan and Aztec monuments, and 55 degrees north is the approximate latitude of northern UK stone circles like Long Meg and her Daughters and Castlerigg… if you want to study monuments in the southern hemisphere, modify the script… similarly, you can modify the script if you just want to look at a specific latitude, or want finer binning in time).  The results are output to the file sun_moon_azi_by_year.out

Note that the calculations assume a flat sea level horizon!  Nearly all sites don’t fit this criterion, which means that the true rise/set azimuth of celestial bodies would have to be corrected for the horizon… this can lead to corrections of several degrees in the actual azimuths.  Thus, the figures below should just be a rough guide as to what to expect.  In a later post, I’ll be talking about how to correct the calculated rise/set azimuths for the horizon profile.

The R script plot_sun_moon_azi_by_lat.R reads in the sun_moon_azi_by_year.out that you download into your local working directory (or obtain by running the sun_moon.R script), and creates the following graphs for the rise and set azimuths: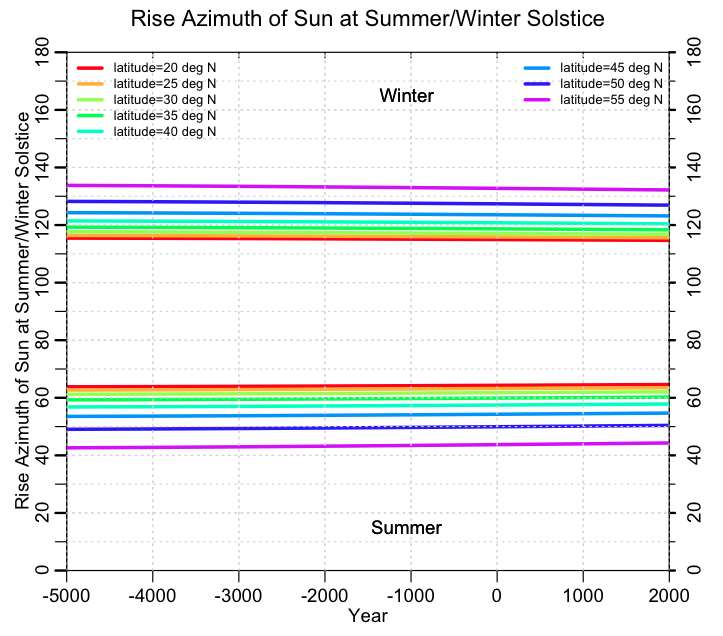

The major moon standstill azimuths, which is the furthest north and south that the moon ever rises at a particular latitude during the 18.6 year lunar cycle (you may be wondering… is there a “lunar arctic circle” latitude above which there is at least one day in time where the moon never sets?  Yes there is… at around 60 degrees North which (a propos of nothing) is the latitude of the Orkney Islands):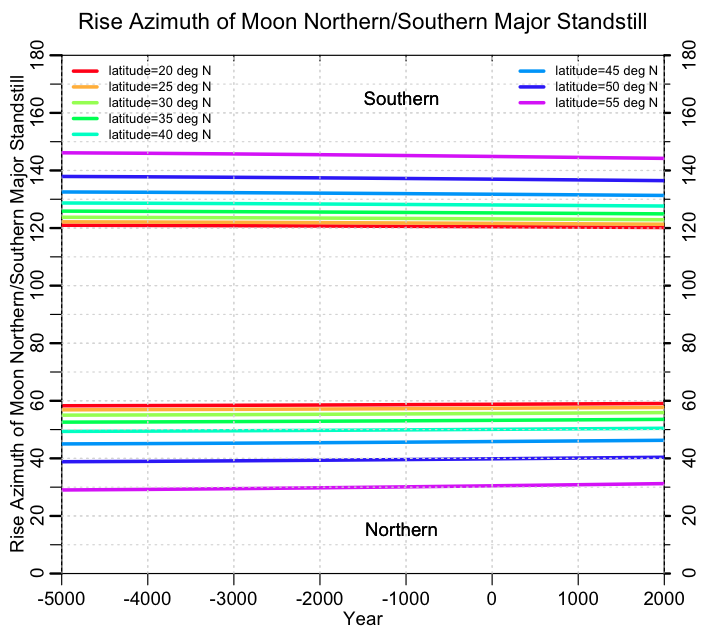

And the minor lunar standstill azimuths: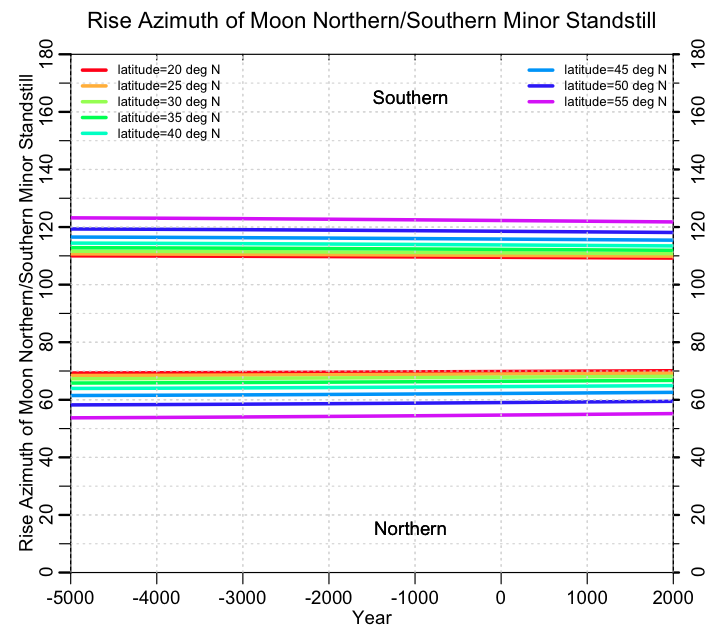

One thing should be clear from these three plots: the sun and moon rise and set azimuths aren’t very sensitive to the date.  At the highest latitudes, the major moon standstill and sun solstices only vary by just a few degrees over 7000 years.  Given that nearly all archaeological sites that are suspected to be astronomical observatories have some degradation of condition that leads to uncertainty in sight lines, it should be obvious that one should not depend on just sun or moon rise/set azimuth angles to try to date a site.

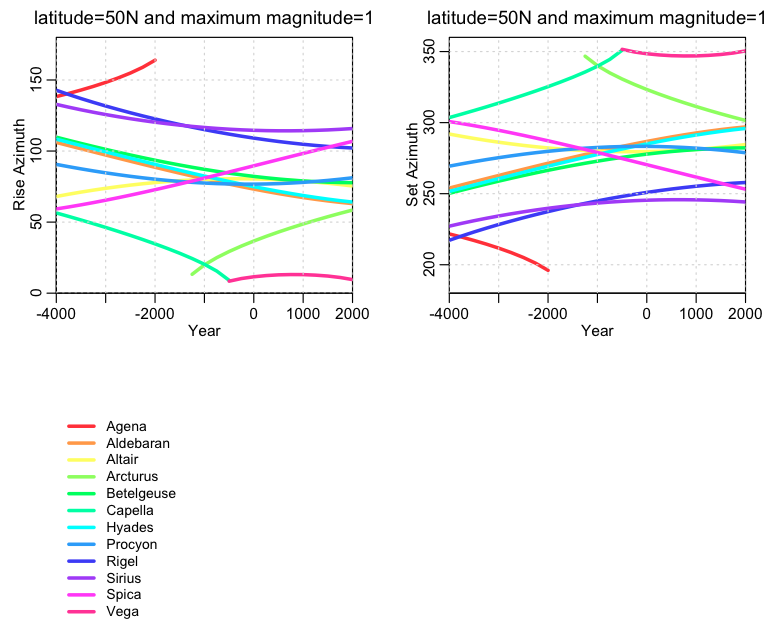
Some stars, however, do change their relative position in the sky by quite a bit over relatively short periods of time (say, 1000 years).  Such stars have a large proper motion.  This website has a little movie that shows how the relative positions of the stars in the big dipper change over time.  This website has a nice list of the proper motions of the brightest stars.  Notice that Arcturus is a very bright star (bright stars have a low magnitude) with a large proper motion.  Capella and Aldebaran are two other bright stars with large proper motion.  In contrast, there are other  bright stars like Vega that move fairly slowly.  However, in a short period of time (say, a couple of generations in the human population) even “fast” moving stars don’t change their rise/set azimuths perceptibly on the horizon.  Within a person’s lifetime, the stars thus always have a seemingly unchanging rise and set azimuth (contrast this to the sun and moon, whose rise and set azimuths are constantly changing… albeit with a predictable pattern).

Even stars with small proper motions will change their rise/set azimuths over time due to the changes in the Earth’s axial tilt.

Thus, if a site has several stellar alignments, alignments to multiple fast moving stars can be used to date the site to fairly good precision.  Picking just one line at a multiple site-line site that happens to align with just one bright star at a particular date is a terrible means of attempting to date the site; the result would not be credible, because the probability of obtaining an alignment like that just by mere random chance is extremely high!

To calculate the rise/set azimuths of stars at a particular date for a place at a particular latitude, I use the pyephem python library for ephemeris calculations. In the python script stars.py I calculate the rise/set azimuths of stars and the sun for latitudes from -60 to +60 in 5 degree increments, for years 4000BC to present in 250 year increments.  The list of stars is the list of all the stars that compromise the pyephem star database (94 in total).

The R script stars.R reads in the output files of the stars.py script and produces the plot for the star rise/set azimuths at 50N is:

Keep in mind that the results for the rise/set azimuths from the star.py script assume a flat horizon; in reality for actual archaeological sites this is very rarely true and horizon effects can change the actual rise/set azimuth of a celestial body by several degrees.  Like I mentioned above, in a later post I will talk about how to correct for horizon effects.