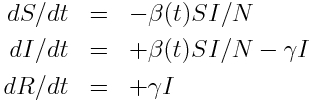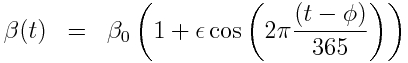[This is part of a series of modules on optimisation methods]

Latin hypercube sampling model parameter optimisation is a computationally intensive algorithm that nonetheless have several advantages over other optimisation methods for application to problems in mathematical epidemiology/biology in that it doesn’t require computation of a gradient.

Once you have chosen an appropriate goodness-of-fit statistic comparing your model to data, you wish to find the model parameters that optimise (minimise) the goodness-of-fit statistic.  Latin hypercube sampling is a computationally intensive “brute force” parameter optimisation method that has the advantage that they don’t require any information about the gradient of the goodness-of-fit statistic.

Latin Hypercube Sampling

With Latin hypercube sampling, you assume that the true parameters must lie somewhere within a hypercube you define in the k-dimensional parameter space.  You grid up the hypercube with M grid points in each dimension.  In the center of each of the M^k points, you calculate the goodness-of-fit statistic.  With this method you can readily determine the approximate location of the minimum of the GoF.  Because nested loops are involved, with use of computational tools like OpenMP, the calculations can be parallelised to some degree.  However, if the sampling region of the hypercube is too large, you need to make M large to get sufficiently granular estimate of the dependence of the GoF statistic on the parameters.  Iterations of the procedure are usually necessary to narrow down the appropriate sampling region.

If you make the sampling range for each of the parameters large enough that you are sure the true parameters must lie within those ranges, with this method you can be reasonably sure that you are finding the global minimum of the GoF, rather than just a local minimum.  This is important, because very often in real epidemic or population data, I have noted local minima in GoF statistics.

Example: fitting to simulated pandemic influenza data

We’ll use as example “data” a simulated pandemic flu like illness spreading in a population, with true model:

with seasonal transmission rate

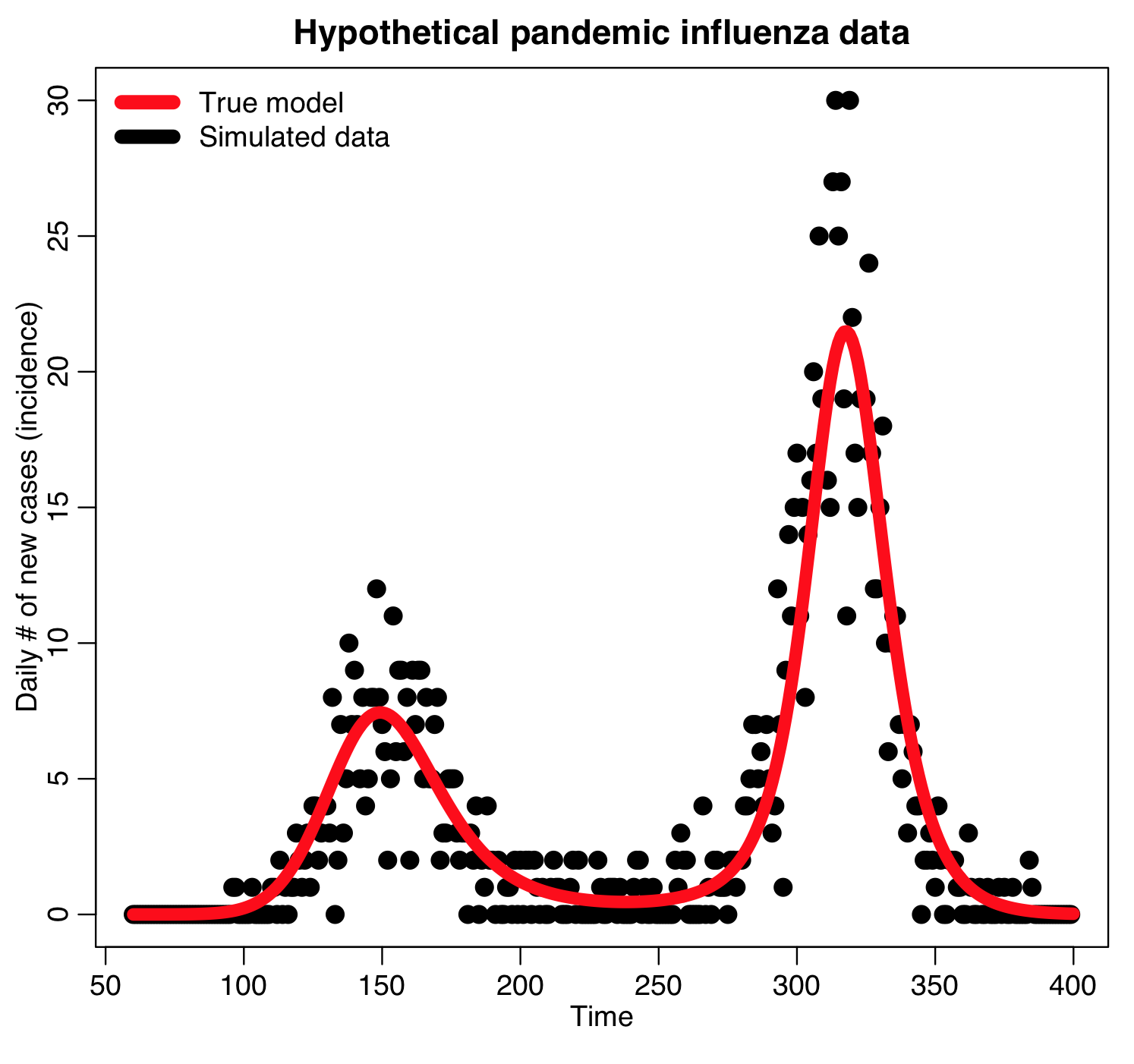
The R script sir_harm_sde.R uses the above model with parameters 1/gamma=3 days, beta_0=0.5, epsilon=0.3, and phi=0. One infected person is assumed to be introduced to an entirely susceptible population of 10 million on day 60, and only 1/5000 cases is assumed to be counted (this is actually the approximate number of flu cases that are typically detected by surveillance networks in the US). The script uses Stochastic Differential Equations to simulate the outbreak with population stochasticity, then additionally simulates the fact that the surveillance system on average only catches 1/5000 cases. The script outputs the simulated data to the file sir_harmonic_sde_simulated_outbreak.csv

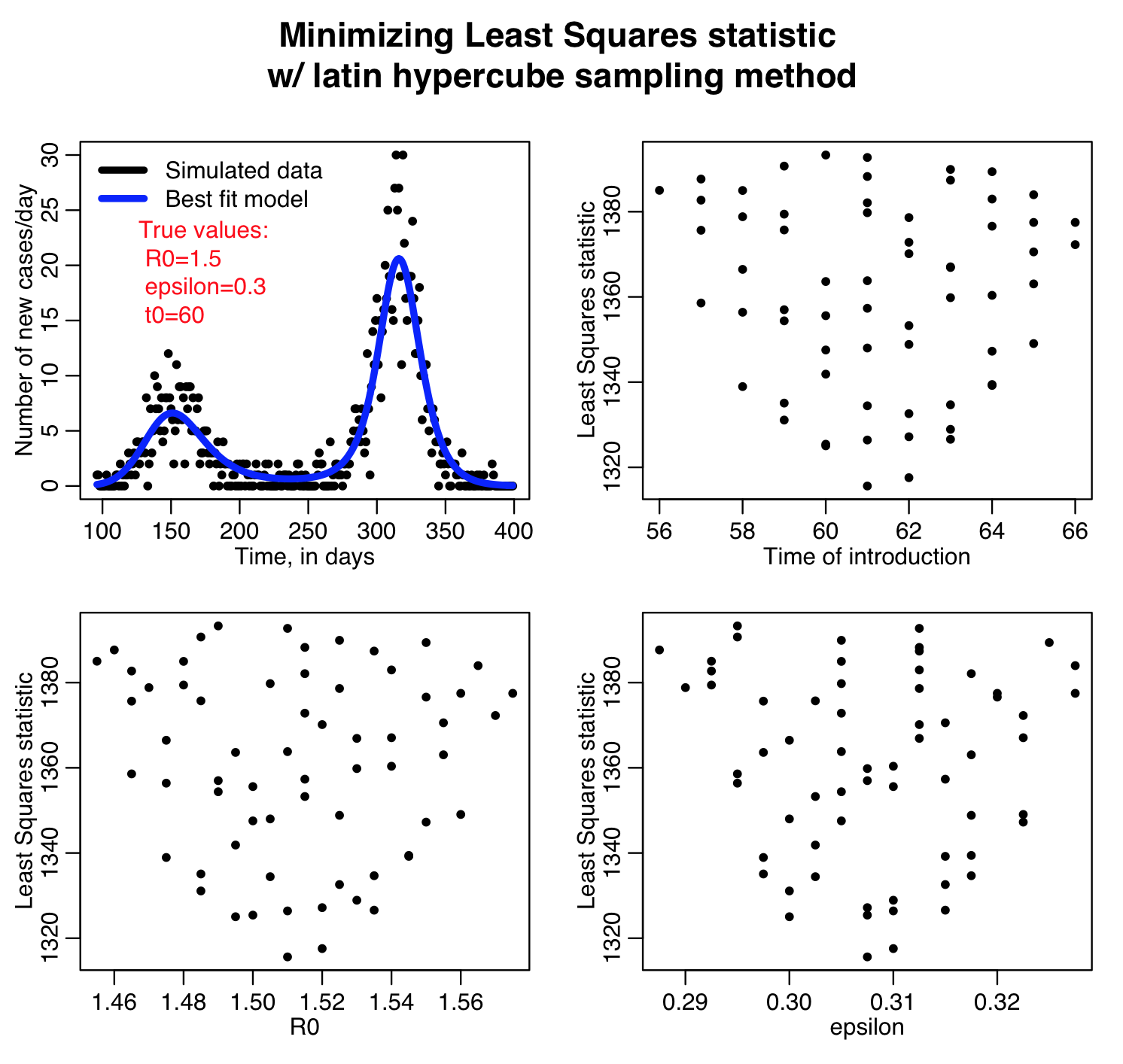
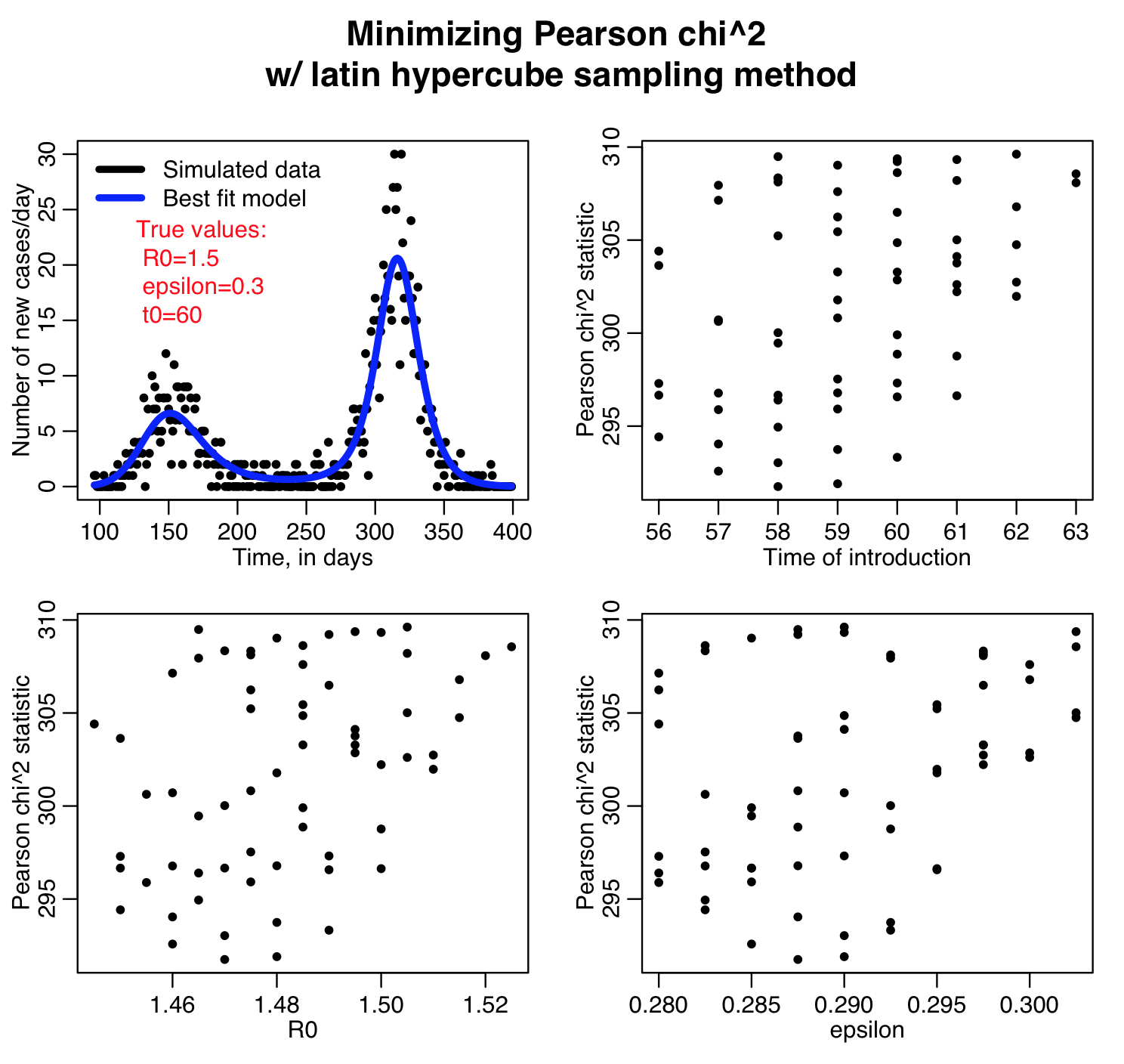
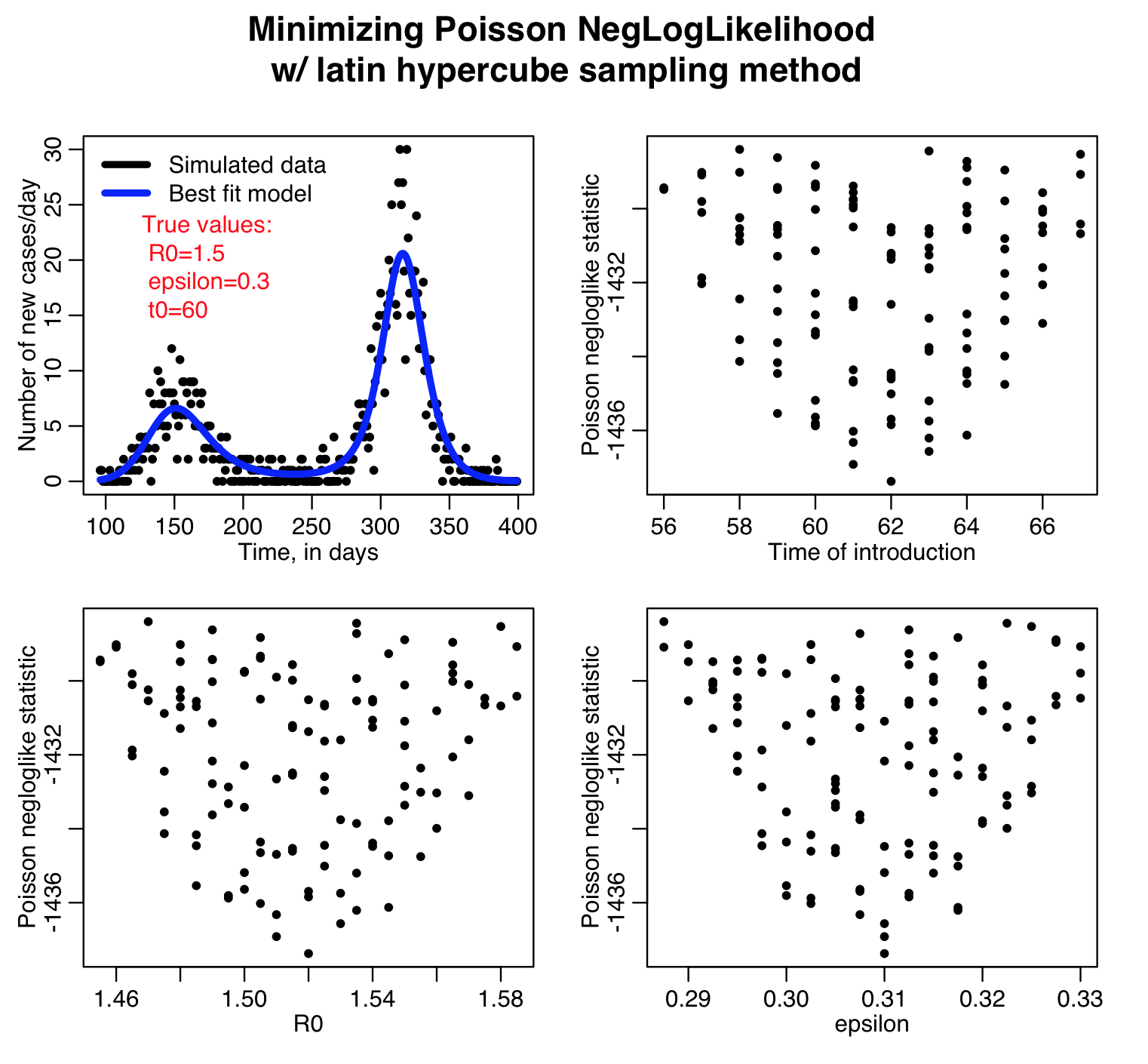
The R script sir_harm_latin_hypercube.R uses the graphical Monte Carlo Latin hypercube method to find the best-fit model to our simulated pandemic influenza data, contained in the file sir_harmonic_sde_simulated_outbreak.csv.  Recall that our simulated data and the true model looked like this:

The sir_harm_latin_hypercube.R script samples:

• discrete values of R0 from 1.44 to 1.59 in steps of 0.005 (31 values total),
• discrete values of t0 from 56 to 67 (12 values total), and
• discrete values of epsilon from 0.28 to 0.34 in steps of 0.0025 (25 values total).
• There are thus M=31*12*25=9300 distinct sets of (R0,t0,epsilon) hypotheses that are tried.

For each set of the hypotheses, the script calculates three different goodness-of-fit statistics (Least squares, Pearson chi-squared, and Poisson negative log-likehood).  Question: this is count data… which of those GoF statistics are probably the most appropriate to use?

How did I know which ranges to use? I ran the script a couple of times and fine-tuned the parameter ranges to ensure that the ranges actually contained the values that minimized the GoF statistics, and that the ranges weren’t so broad that I couldn’t really tell were the best-fit values were.

The script outputs the following plots:

The Latin hypercube sampling method is not that easily parallelisable to make use of high performance computing resources, but if implemented in C++ there is the possibility that OpenMP can be used for process threading.  It also has the disadvantage that the granularity in the discrete sampling produces sparse plots that make it difficult to reliably estimate the best-fit parameters and the uncertainties on those estimates.

Latin hypercube sampling does have the advantage that Bayesian priors on the model parameters can trivially be applied post-hoc to the results of the parameter sampling to assess the effect the priors have on the parameter estimate uncertainties.